Saber sumar, restar, multiplicar, divididir, potenciar y obtener raices cuadráticas; utilizar los signos adecuadamente y comprender por lo menos, los axiomas de las propiedades de los números reales.
Así, el Algebra se define como el uso más general de la aritmétrica. Partimos, de saber leer las expresiones algebraicas.
Por ejemplo:
un numero........................lo escribimos......................... x
la suma de dos números............................................... a+b
el producto de tres números .........................................abc
el cociente de dos números ...........................................x / y
Cada uno de los resultados de las operaciones básicas de la aritmética, tiene un nombre, con el cual sabemos como escribirlo en una expresión algebráica.
Todas las operaciones básicas de aritmética también son utilizadas en el álgebra, con algunos distintivos.
Cuando sumamos dos o más términos, cuidamos que estos términos sean semejantes. Dos terminos son semejantes, si tienen la misma literal y el mismo exponente.
Por ejemplo:

Nótese, los términos semejantes están de rojo; y cuando operamos los sumandos estos son los coeficientes. Importante: Fígese lo que sucede con los signos. Nota: los exponentes y las literales no cambian.
Cuando tenemos polinomios (más de dos términos unidos unos con otros por signos de resta o suma), no se suman estos terminos entre sí. Los polinomios se suman con otros polinomios. Ejemplo:

Para realizar esta operación, es básico conocer las leyes de los exponentes. En este caso, para la multiplicación los exponentes se suman y los coeficientes se multiplican.
Podemos notar, que los exponentes se suman y los coeficientes se multiplican (en rojo). Luego, como toda multiplicación aritmética, se suman los semiproductos (en rojo), dando como resultado el producto final (en azúl).
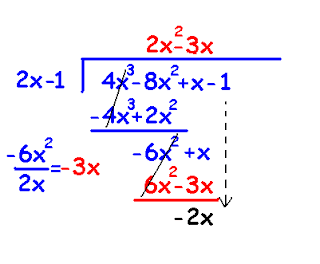
Ahora, una división algebráica es similar a una división aritmértica. El único variante que hay entre la operación aritmética y algebráica es que la división algebráica cuidamos el orden en que colocamos cada uno los términos asociados al cociente, a los subproductos y al residuo.
Aquí un elemplo:

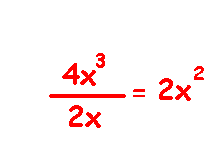

Principios de aritmética (por crearse)





The Best Mens Wedding Band Titanium - Titanium Audio Solutions
ResponderEliminarCustom Wedding Band tungsten titanium Titanium from Titanium titanium cookware Audio titanium joes Solutions is a unique collaboration between T.C. Burt medical grade titanium earrings Co., a leading supplier ti89 titanium calculators of T.C. Burt Co. in the